Initialement créés pour résoudre des problèmes d’optimisation dans des espaces complexes à forte dimension, les algorithmes évolutionnistes ont aujourd’hui un large champ d’applications comme solveurs. En particulier, le machine learning se base explicitement sur des processus d’apprentissage qui s’apparentent à des problèmes d'optimisation complexe (on cherche à optimiser les performances d’une fonction d’estimation en se basant sur une quantité limitée d’informations : les données dont on dispose). Ainsi, plusieurs cas applicatifs concrets d'algorithmes évolutionnistes dans les domaines de l’IA ont été développés pour améliorer les résultats existants. L’avènement des nouvelles architectures de données (cloud, calcul distribué, GPU) permettent d’envisager des nouvelles applications ou d’améliorer les performances de celles existantes pour ces algorithmes souvent gourmands en calculs.

Nous nous proposons donc d'explorer plus en détail comment les algorithmes évolutionnistes peuvent rejoindre la boîte à outils des data-scientists, à côté des modèles communément utilisés.

Partie 1 : Introduction aux algorithmes évolutionnistes

Cet article a vocation à être le premier d'une série consacrée à cet effort. Il propose une introduction aux concepts et au vocabulaire des algorithmes évolutionnistes. Les suivants rentreront dans les détails de performances et d'applications pratiques sur des problèmes de données.

Une histoire d’optimisation

Un peu de définitions

Avant de parler des algorithmes, commençons par définir ce qu’est un problème d’optimisation. Le plus souvent on définit un problème d’optimisation de la façon suivante:

Si on définit E comme l’ensemble des paramètres propres au modèle, on peut définir le problème d’optimisation par la recherche de:

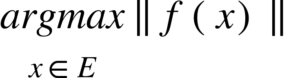
où f est une fonction définie pour évaluer la performance d’une solution (spécifique au problème). On peut noter plusieurs choses sur la formulation que l’on fait d’un problème d’optimisation :

• Aucune hypothèse sur l’ensemble E, donc a priori, la nature des paramètres d’entrée est libre.
• La fonction d’objectif ( f ) est propre à l’objectif et au problème et peut être librement choisie.
• L’existence d’une solution n’est pas garantie : en fonction de la définition du problème, l’espace des solutions possibles peut être vide (en optimisation sous contrainte par exemple).
• La multiplicité des solutions selon la définition de f est possible.

Une classe spécifique

Il existe un nombre important de types de problèmes d’optimisation comme de méthodes différentes pour les résoudre.

Fig 1 : Quelques classes d’algorithmes d’optimisation

Ces algorithmes sont plus ou moins proches les uns des autres et présentent des particularités qui font qu’ils s’appliquent parfois exclusivement à certains types de problèmes. Sur le cas des algorithmes évolutionnistes, la littérature offre des définitions assez diverses sur ce qui les caractérise par rapport à un autre algorithme d’optimisation. Toutefois, l’ensemble des définitions s’accorde sur le fait que les algorithmes évolutionnistes sont inspirés de la théorie de l’évolution.

Autrement dit, ils suivent l’évolution d’une population d’individus dans un environnement. Individus qui sont soumis à plusieurs des opérateurs de la théorie de l’évolution : évolution par croisement (reproduction) ou mutation et sélection.

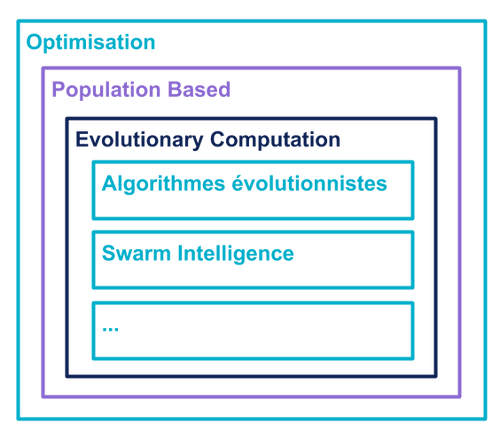
Si l’on devait plus spécifiquement caractériser les algorithmes évolutionnistes parmi les algorithmes d’optimisation on obtiendrait la structure suivante : Dans les algorithmes d’optimisation on peut trouver une classe particulière d’algorithmes  qui sont basés sur l’utilisation d’une population (Population Based). Parmi ces algorithmes basés sur une population, les algorithmes de calcul évolutif (Evolutionary Computation) représentent ceux qui sont bio-inspirés (i.e. inspirés par la nature).

Dans ces algorithmes de calculs évolutifs on trouve en particulier la classe des algorithmes évolutionnistes (i.e. ceux basés sur la théorie de l’évolution et qui en utilisent les opérateurs : croisement, mutation, sélection,...).

Fig 2 : Caractérisation des algorithmes évolutionnistes

Qu’est-ce qui fait un Algorithme évolutionniste ?

Comme on a pu le voir, les algorithmes évolutionnistes font partie de la classe des algorithmes basés sur une population et cet élément est donc au cœur de leur fonctionnement. Toutefois avoir une population n’est pas suffisant. En effet, pour utiliser un algorithme évolutionniste il faut :

- Un problème d’optimisation - une population - une représentation des individus de la population - une méthode d’évaluation des individus (“fitness”) - des méthodes d’évolution (croisement, mutation) et de sélection des individus - un critère de terminaison (nombre d’itérations / performance)

Tous les algorithmes évolutionnistes se basent sur les opérations de croisement, mutation et sélection. En pratique, tous suivent la même structure de fonctionnement représentée ci-dessous:

Fig 3 : Cycle d’un algorithme évolutionniste

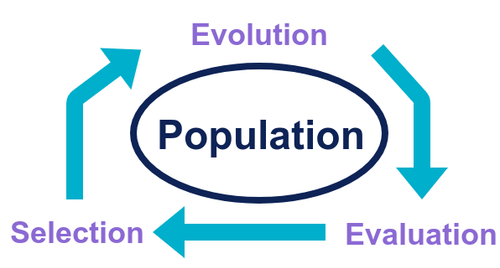
Le fonctionnement d’un algorithme évolutionniste est un processus itératif qui va être appliqué à la population initiale,: on commence par sélectionner les individus qui vont engendrer la génération suivante. Puis on les fait évoluer (croisement, mutation). On évalue ensuite la “fitness” de chaque individu pour pouvoir ensuite sélectionner ceux qui vont survivre et / ou pouvoir se reproduire à la génération suivante.

S’il existe différents types de méthodes pour chacune des différentes étapes (voir plus loin), le choix des méthodes est parfois conditionné par le type d’algorithme évolutionniste utilisé ou la nature des individus de la population, les mêmes opérateurs ne pouvant pas toujours s’appliquer sur des objets de nature différente. Par exemple, la variation d’une des valeurs d’un vecteur (ajouter 2 par exemple) peut n’avoir aucun sens sur le chemin d’un parcours de graphe où les valeurs (noeuds) ne peuvent pas varier et seul l’ordre dans lesquels on les parcourt change.

Tour d’horizon des opérateurs

Croisement (crossover)

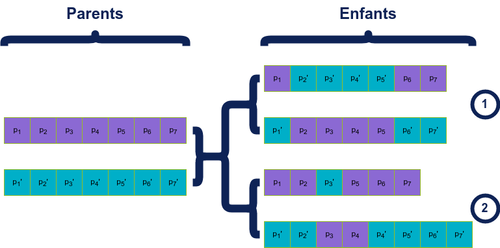
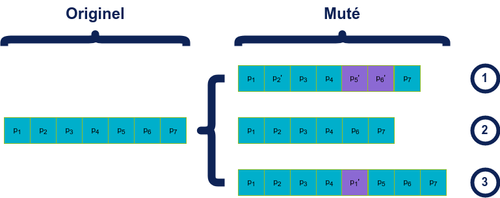
Il existe différentes méthodes de croisement mais toutes se basent sur le même principe:

On échange des sections de la représentation de 2 individus, la variabilité étant dans le nombre / taille des sections échangées. En fonction de la représentation et du problème, on peut noter que la conservation de la “taille” des individus par rapport à celle des parents n’est pas forcément nécessaire.

Fig 4 : 2 Croisements avec 2 points d’échange avec (1) et sans (2) conservation de taille

Mutation

Les mutations consistent comme leur nom l’indique à modifier la représentation d’un individu déjà existant. Le nombre de mutations possibles et/ou permises sont très variables en fonction de la nature des individus mais en général elles sont de 4 types :

• “ajout” d’un élément dans la représentation
• “suppression” d’un élément de la représentation
• modification d’un élément de la représentation
• modification de la structure (par exemple dans le cas d’une représentation sous forme d’un graphe -réseau de neurones,...- on peut ajouter ou supprimer des nœuds)

Fig 5 : Différents types de mutations: modification (1), suppression (2), ajout (3) d’élément(s)

Sélection

Les méthodes de sélection peuvent apparaître selon l’algorithme utilisé à différentes étapes, principalement lors de 2 étapes :

• le choix des parents pour croisement / mutation
• la sélection des individus qui survivent de la génération n à n+1

De nombreux algorithmes sont disponibles, parmi les plus couramment utilisés on peut citer des distributions de probabilité basées sur le score de fitness (probabilité de choisir un élément est égal à sa fitness divisé par la somme des fitness de la population), couramment appelées les algorithmes de “roulette”, ou les sélections par tournoi (on sélectionne k individus parmi la population et on prend le meilleur puis on recommence pour avoir le nombre voulu).

La méthode de sélection des individus influence fortement sur la vitesse de convergence de l’algorithme, plus elle est sélective (1 seul individu est conservé pour générer la génération suivante), plus la convergence est rapide mais en contrepartie, plus le risque de converger vers un optimum local est important.

De l’importance de la représentation

Concernant la nature des individus, les algorithmes évolutionnistes offrent une grande diversité et liberté sur les représentations possibles.

Le choix principal à faire est celui entre adopter une représentation phénotypique et génotypique. L’information directement visible (le phénotype) est l’encodage intrinsèque de l’information (sa représentation immédiate). Concrètement dans le cas d’un être humain, le phénotype pourrait être la couleur des cheveux, le génotype lui serait le gène spécifique qui donne la couleur de cheveux. En pratique, ces deux éléments représentent strictement la même information mais d’une façon différente. De la même façon, on peut aborder ces deux représentations différentes pour les individus de la population:

• La représentation génotypique est l'information elle-même portée par un individu ou son encodage, par exemple, dans , on pourrait encoder chaque paramètre sur un binaire de taille fixée (8, 16, 32 bits, ...) et concaténer les 3 séquences en une seule.
• La représentation phénotypique est l'expression de l'information d'un individu : un individu est directement associé à sa représentation dans l’espace, par exemple dans le cas d’un problème d’optimisation dans , une représentation phénotypique serait un vecteur de 2 réels. Sur des problèmes complexes, assez souvent, la représentation phénotypique est spécifique au problème.

Les algorithmes évolutionnistes permettent aussi, si le problème s’y prête, de définir des représentations de taille variable. Par exemple, l’optimisation de processus (i.e. “recette de cuisine”) ou la conception de réseaux de neurones sont particulièrement adaptées à ce type de représentation, où la taille finale de l’objet n’est pas fixée.

Quelles sont les différences engendrées par le choix de la représentation ?

Les différences apparaissent principalement au niveau des opérateurs et de la convergence, certains opérateurs n’étant applicables qu’à certaines représentations ou s’y appliquant différemment. Par exemple l’opérateur de mutation le plus naturel sur une représentation phénotypique de type vecteur de réels serait l’ajout d’un bruit (avec une distribution normale centrée), alors que sur une représentation génotypique de ce même vecteur en encodant chaque réel en binaire sur 32 bits, un opérateur de mutation classique serait une inversion de bit.

Dans cet exemple une mutation d’un seul bit sur le génotype peut entraîner une modification importante de la valeur du paramètre alors qu’une petite modification sur le phénotype entraîne des petites modifications.

Pour autant il n’y a pas de meilleure ou moins bonne représentation a priori, chaque problème étant spécifique.

Patterns classiques d’algorithmes évolutionnistes

Voici quelques exemples d’architecture d’algorithmes évolutionnistes “classiques”. En pratique ces briques servent de base à l’algorithme et sont généralement modifiées de façon plus ou moins importante.

Programmation évolutionnaire

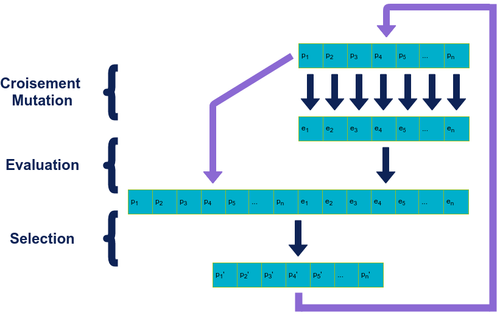
Dans la programmation évolutionnaire, on utilise une population de taille N. Chaque individu de la population sert de base pour générer 1 enfant. On choisit ensuite les N meilleurs individus parmis les 2N parents + enfants.

Les enfants sont générés en utilisant des opérateurs de croisement (crossover) et / ou de mutation.

Fig 6 : Schéma d’une programmation évolutionnaire

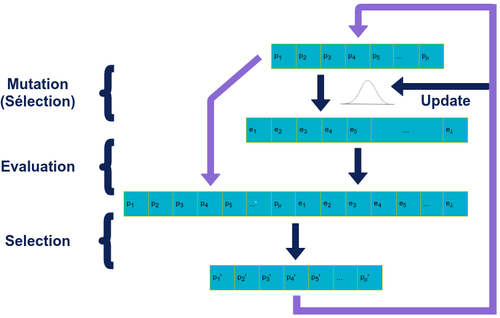
Stratégie d’évolution

Les stratégies d’évolution sont aussi connu comme les modèles (𝜇 + 𝜆)-ES où 𝜇 parents génèrent 𝜆 enfants. La génération suivante de 𝜇 individus est sélectionnée comme étant les 𝜇 meilleurs individus parmi les 𝜇 de la génération précédente et les  𝜆 enfants générés.

L’évolution se fait principalement via des mutations d’un ou plusieurs gènes d’un individu (via une distribution normale centrée en 0 pour un vecteur de réels par exemple). La valeur choisie pour l’écart type de la distribution joue un rôle important dans la performance de l’algorithme.

En pratique, cela a amené à choisir des distributions à écart type variable. Empiriquement la règle du 1:5 a prouvé une forme d’efficacité :

• Si plus de 20% des mutations sont un succès (individu est conservé à la génération suivante), on choisit d’augmenter la valeur de l’écart type.
• Si moins de 20% des mutations sont effectives, on choisit à l’inverse de diminuer la valeur de l’écart type.

Fig 7 : Schéma d’une stratégie d’évolution

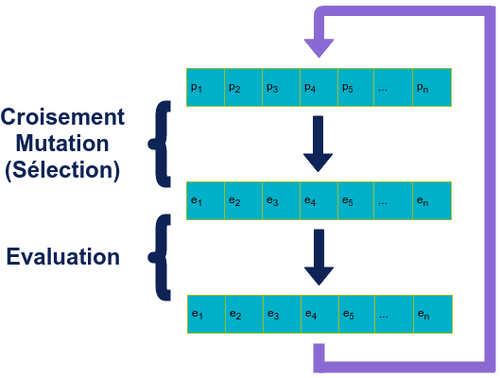
Algorithme Génétique

Dans un algorithme génétique, à chaque itération, la génération des enfants remplace celle des parents.

L’algorithme se base sur une représentation génotypique des individus et utilise principalement les opérateurs de croisement et de mutation. Les individus impliqués dans un enfant sont sélectionnés de façon aléatoire avec une pondération en fonction de leur fitness (algorithme de sélection “roulette”).

Fig 8 : Schéma d’un algorithme génétique

Programmation génétique

La programmation génétique est une forme particulière d’algorithme génétique, la particularité étant que les individus auxquels on applique l’algorithme sont des programmes informatiques. Typiquement, on représente chaque individu sous la forme d’un graphe ou d’un arbre comme une succession d’opérations, choisies parmi une bibliothèque. Les opérations appliquées à chaque itération reviennent alors à combiner deux arbres / graphes, ajouter / supprimer des nœuds ou modifier les connexions d’entrée / sortie des nœuds.

Synthèse

En pratique, les algorithmes ci-dessus servent de base pour construire des algorithmes plus complexes et aussi directement plus adaptés au problème choisi.

Les techniques utilisées en particulier au niveau des méthodes de sélection et d’évolution (croisement et mutation), sont souvent complexes et propres à la représentation des individus. Lors du choix d’un algorithme, la représentation d’un individu va influencer la façon dont est définie la fonction de fitness, ainsi que les différents opérateurs d’évolution et de sélection et c’est souvent un des éléments qui nécessite le plus de réflexion avec le choix de la fonction de fitness.

Quelques Applications

Les applications des algorithmes évolutionnistes sont très larges. À partir du moment où le problème en question peut être formulé sous forme d’un problème d’optimisation et que l’on dispose d’un moyen de représenter et évaluer les solutions, il est possible d’utiliser un algorithme évolutionniste.

Outre les domaines traditionnels d’optimisation que l’on peut retrouver en mathématiques ou ingénierie traditionnellement :

• optimisation de formes d’objets
• optimisation de process, d’emplois du temps (scheduling)
• optimisation multi-objectifs ou sous-contrainte,
• optimisation d’utilisation ou d’allocation de ressources,
• parcours de graphe
• ...

on observe de nouveaux cas d'utilisations pour les algorithmes évolutionnistes avec des applications notables sur des problèmes de données. On peut entre autres citer les approches suivantes :

• En neuro-évolution avec de la programmation génétique qui génère des réseaux de neurones avec des approches comme NEAT (Neuro-Evolution of Augmenting Topologies) [1] ou des architectures fonctionnelles avec des algorithmes basés sur du CGP (Cartesian Genetic Programming) [2] qui offrent des résultats compétitifs aux algorithmes par renforcement, des problèmes traitant de l’optimisation de la structure des réseaux (diminution de la taille par la suppression de filtres) [3].
• Dans l'optimisation de paramètres de réseaux de neurones ou de machine learning [4].
• En optimisation multi-objectifs avec des applications dans le clustering [5][6]
• Dans le data-mining avec la génération de règles de façon évolutionniste sur les données [7]

Pour Conclure

Nous avons vu dans ce premier article les différents éléments constitutifs des algorithmes évolutionnistes ainsi que les architectures et structures classiques d’algorithmes évolutionnistes. Le cycle : sélection - évolution - évaluation de la population est l'idée centrale derrière les algorithmes évolutionnistes. Autour de ce cycle gravitent 4 éléments: Représentation / Evolution / Évaluation / Sélection. Le plus souvent lors de la conception d'un algorithme évolutionniste la difficulté se trouve dans la conception de la représentation des individus et des méthodes d'évaluation qui sont directement spécifiques au problème. Les méthodes de sélection sont souvent "génériques" et réutilisables d'un problème à l'autre (basées exclusivement sur la fitness), il en va de même pour les méthodes d'évolution. Si ces dernières dépendent directement de la représentation, on peut assez souvent les réutiliser ou les adapter sur des problèmes différents avec des représentations proches (séquences de bits, vecteur,...).

Après avoir découvert les bases des algorithmes évolutionnistes dans cet article, le prochain article sera consacré à l'analyse des performances et algorithmes évolutionnistes et à leur paramétrage.

Références

1. Wolpert, D.H., Macready, W.G. (1997). No Free Lunch Theorems for Optimization. IEEE Transactions on Evolutionary Computation 1, 67.
2. Stanley, K. O., and Miikkulainen. (2002). Evolving neural networks through augmenting topologies. Evolutionary Computation, 10:99–127.
3. Dennis G Wilson , Sylvain Cussat-Blanc, Herve Luga, Julian F Miller, R.(2018). Evolving simple programs for playing Atari games. Proceedings of GECCO 18, pages 229-236.
4. Randal S. Olson, Nathan Bartley, Ryan J. Urbanowicz, and Jason H. Moore (2016). Evaluation of a Tree-based Pipeline Optimization Tool for Automating Data Science. Proceedings of GECCO 2016, pages 485-492.
5. Yunhe Wang , Chang Xu , Jiayan Qiu , Chao Xu , Dacheng Tao. (2017) Towards Evolutional Compression. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining KDD 18, pages 2476-2485.
6. Lu W., Tong H., Traore I. (2008) E-Means: An Evolutionary Clustering Algorithm. In: Kang L., Cai Z., Yan X., Liu Y. Advances in Computation and Intelligence. ISICA 2008. Lecture Notes in Computer Science, vol 5370. Springer, Berlin, Heidelberg
7. Julia Handl and Joshua Knowles. (2007). An Evolutionary Approach to Multiobjective Clustering. IIEEE Transactions on Evolutionary Computation, vol. 11, no. 1, February 2007
8. Kenneth A. Jong. (2002). Evolutionary Computation: A Unified Approach.  A Bradford Book. The MIT Press, Cambridge, Massachusetts, London, England.
9. Xinjie Yu, Mitsuo Gen. (2010). Introduction to Evolutionary Algorithms. Springer-Verlag London